債券的彎曲度—續1(Bond Convexity)
這篇文章,我們來看一個例子。
債券A,面額100,到期時間15年,每年配息一次,票面利率8%。
債券B,面額100,到期時間10年,每年配息一次,票面利率0%。
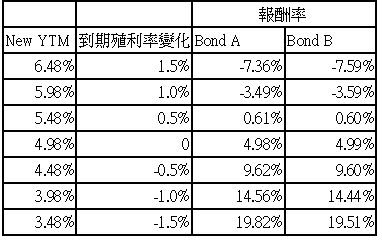
兩張債券都處在到期殖利率(YTM)4.98%的狀況下。如下表:
(此例取材自Douglas Hearth等人所著Contemporary Investments一書)
由這些資料,我們可以算出這兩張債券的存續時間(Macaulay duration)都是10年,但曲率方面,債券A較高是123.42,債券B則是99.8。
我們分別持有債券A和B一年,這一年後,到期殖利率也產生了改變。我們可以算出這一年來的報酬(Holding period return)。
這個表格中分別模擬了殖利率上升1.5%到下跌1.5%的狀況。我們可以看到,當殖利率漲到6.48%,比原先的4.98%高了1.5%的時候,無論債券A還是債券B都產生了損失,但債券A損失較少。
當殖利率下跌到3.48%時,兩張債券都賺錢,而且債券A賺比較多。
這個例子有幾個重點。
首先,我們再次看到了曲率較大的債券,升息時損失較少,降息時獲利較大。
再來,我們發現升降息幅度愈大,債券A與債券B的報酬率差異就會愈大。
最後則是,這兩張債券的存續時間相同,都是十年。而存續時間是用來衡量債券價格對利率變動的敏感度。存續時間長的債券,面對相同的利率變化,價格會有較大的波動。但我們看到,這兩張存續時間相同的債券,它們對利率變動產生的價格變化是不一樣的。
為什麼會這樣?
因為存續時間是一個估計。
我們一樣可以看個簡圖,掌握這個概念。
紅線表某債券的價格與到期殖利率關係。
我們先看在到期殖利率5%的那個點。我們在到期殖利率5%那點,對這個曲線做一條切線。這條切線的斜率,就是存續時間。
使用存續時間估算債券價格對利率的變化,就是用這條切線在估算。
我們可以看到,當到期殖利率升到6%時,曲線指出的實際價格減損,會比那條切線少。當殖利率降到4%時,實際的債券價格增值會比切線多。兩者的差距,以藍線表示。
所以,使用存續期間進行估算,當降息時,會低估債券的增值幅度。升息時,則會高估債券的降值程度。
從這個圖還可以看出幾個概念。首先就是殖利率變動的幅度愈少,使用存續時間的估算與真實情況差距愈小。換句話說就是,使用存續期間估算,在大幅度的殖利率變動下,會嚴重失真。還有,對曲率大的債券使用存續期間估算,會產生較大的偏差。
知道了這些之後,就能瞭解例子中為什麼A債券和B債券的存續期間相同,卻對利率變化有不同程度的反應,也知道為什麼當利率變動愈大時,兩者報酬的差距愈大。
待續..
點一下,推一下:
回到首頁:請按這裡
初來乍到:請看”如何使用本部落格”
相關文章:
債券的彎曲度(Bond Convexity)
債券的彎曲度—續2(Bond Convexity)
債券的存續期間—Macaulay Duration
債券的存續期間—Modified Duration
債券基金的主要風險
Labels: 債券






7 comments:
理論上, 看來可以用曲度來套利. (如果可以放空債券的話)
可是實際上利率變動要多大才能夠產生足夠付交易成本的價差呢?
可以請問你是要如何套利呢?
在交會點(利率4.98%), 同時買A賣B.
靜待利率變化之後再平倉(同時賣A買B).
以表中利率最大變動的情況下, 只有0.2~0.3%再除以2的獲利率, 扣掉價差和手續費, 應該是沒得賺.
所以除非利率變動極大, 遠超過表中所列的, 才有機會產生足夠的利差.
計算一下可以得到以下觀點, 曲度在實務上來說, 影響比賦稅考量要小得多.
謝謝分享
還蠻有趣的
這個作法看來是duration-neutral的方法
但問題是
殖利率變化常不是parallel shift
Parallel shift指的是各年期的債券殖利率變化幅度全都一樣
實際上
各年期債券的殖利率變化 常不相同 (或甚至反向也有可能)
假如出現15年期的債券A殖利率上升
10年期的債券B殖利率下降的狀況
那就虧錢了
確實有殖利率變化不一致的可能性.
不過從過去的記錄來說, 長期債的殖利率波動幅度通常比短期債來得大.
不過這樣就幾乎沒有用到曲度的效果了.
也就是說, 在實務上的考量, 曲度是否很少被考慮到? (對價格的影響力相對來說太小)
能否舉例一下
那一個國家 那段期間
長期債券的殖利率波動通常比短期債來得大?
第一, 是短期債券的殖利率變動幅度較大, 寫反了, 不好意思.
第二, 殖利率變動對長期債券價格影響較大.綜合一和二, 長期債券的價格波動仍然較大.
第三, 長期債券殖利率通常比短期債券高, 如果兩者接近或相反, 應該會是很好的機會.
整體來看, 曲度似乎很少被考慮到.
張貼留言